The microscopic world is governed by quantum mechanics. This becomes important at low temperatures and strong magnetic fields where more interesting things can happen. It’s useful to distinguish between two different quantum Hall effects which are associated to two related phenomena. These are called the integer and fractional quantum Hall effects. Both were first discovered experimentally and only subsequently understood theoretically

Integer Quantum Hall Effect

The first experiments exploring the quantum regime of the Hall effect were performed in 1980 by von Klitzing, using samples prepared by Dorda and Pepper.

Measurements of the Hall voltage of a two-dimensional electron gas, realized with a silicon metal-oxide-semiconductor field-effect transistor, show that the Hall resistance at particular, experimentally well-defined surface carrier concentrations has fixed values which depend only on the fine-structure constant and speed of light, and is insensitive to the geometry of the device.

The resistivities look like this:

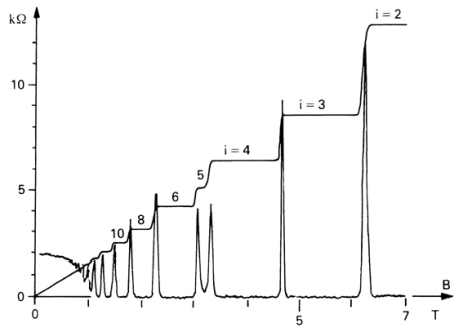
This is the integer quantum Hall effect. For this, von Klitzing was awarded the 1985 Nobel prize. Both the Hall resistivity ρxy and the longitudinal resistivity ρxx exhibit interesting behaviour. Perhaps the most striking feature in the data is the that the Hall resistivity ρxy sits on a plateaux for a range of magnetic field, before jumping suddenly to the next plateau. On these plateau, the resistivity takes the value

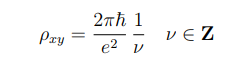
The value of ν is measured to be an integer to an extraordinary accuracy — something like one part in 10⁹. The quantity 2πħ/e² is called the quantum of resistivity (with −e, the electron charge). It is now used as the standard for measuring of resistivity. Moreover, the integer quantum Hall effect is now used as the basis for measuring the ratio of fundamental constants 2π ħ/e² sometimes referred to as the von Klitzing constant. This means that, by definition, the ν = 1 state in the first equation is exactly integer!

The centre of each of these plateaux occurs when the magnetic field takes the value

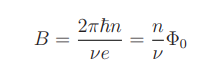
where n is the electron density and Φ₀ = 2πħ/e is known as the flux quantum. These are the values of the magnetic field at which the first ν ∈ Z Landau levels are filled. In fact, as we will see, it is very easy to argue that the Hall resistivity should take value ρ_xy when ν Landau levels are filled. The surprise is that the plateaux exists, with the quantization persisting over a range of magnetic fields. There is a clue in the experimental data about the origin of the plateau.

Experimental systems are typically dirty, filled with impurities. The technical name for this is disorder. Usually one wants to remove this dirt to get at the underlying physics. Yet, in the quantum Hall effect, as you increase the amount of disorder (within reason) the plateaux become more prominent, not less. In fact, in the absence of disorder, the plateaux are expected to vanish completely. The longitudinal resistivity ρ_xx also exhibits a surprise.

When ρ_xy sits on a plateau, the longitudinal resistivity vanishes: ρ_xx = 0. It spikes only when ρ_xy jumps to the next plateau. Usually we would think of a system with ρ_xx = 0 as a perfect conductor. But there’s something a little counter-intuitive about vanishing resistivity in the presence of a magnetic field. To see this, we can return to the simple definition which, in components, reads

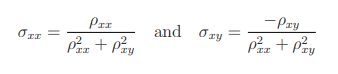
If ρ_xy = 0 then we get the familiar relation between conductivity and resistivity: σ_xx = 1/ρxx. But if ρ_xy ≠ 0, then we have the more interesting relation above. In particular, we see

ρ_xx = 0 ⇒ σ_xx = 0 (if ρ_xy ≠ 0)

While we would usually call a system with ρ_xx = 0 a perfect conductor, we would usually call a system with σ_xx = 0 a perfect insulator!

This particular surprise has more to do with the words we use to describe the phenomena than the underlying physics. In particular, it has nothing to do with quantum mechanics: this behavior occurs in the Drude model in the limit τ → ∞ where there is no scattering. In this situation, the current is flowing perpendicular to the applied electric field, so E · J = 0. But recall that E · J has the interpretation as the work done in accelerating charges. The fact that this vanishes means that we have a steady current flowing without doing any work and, correspondingly, without any dissipation. The fact that σ_xx = 0 is telling us that no current is flowing in the longitudinal direction (like an insulator) while the fact that ρ_xx = 0 is telling us that there is no dissipation of energy (like in a perfect conductor).

Fractional Quantum Hall Effect

As the disorder is decreased, the integer Hall plateaux become less prominent. But other plateaux emerge at fractional values. This was discovered in 1982 by Tsui and Störmer using samples prepared by Gossard.

The resistivities look like this:

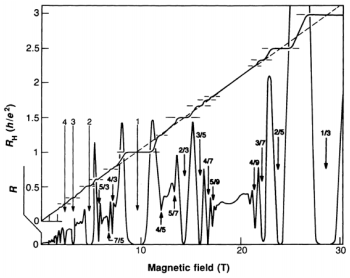
The is the fractional quantum Hall effect. On the plateaux, the Hall resistivity again takes the simple form

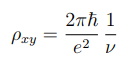
but now with ν a rational number ν ∈ Q Not all fractions appear. The most prominent plateaux sit at ν = 1/3, 1/5 (not shown above) and 2/5 but there are many more. The vast majority of these have denominators which are odd. But there are exceptions: in particular a clear plateaux has been observed at ν = 5/2. As the disorder is decreased, more and more plateaux emerge. It seems plausible that in the limit of a perfectly clean sample, we would get an infinite number of plateaux which brings us back to the classical picture of a straight line for ρ_xy!

The integer quantum Hall effect can be understood using free electrons. In contrast, to explain the fractional quantum Hall effect we need to take interactions between electrons into account. This makes the problem much harder and much richer. The basics of the theory were first laid down by Laughlin, but the subject has since expanded in a myriad of different directions. The 1998 Nobel prize was awarded to Tsui, Störmer and Laughlin.

Materials

The integer quantum Hall effect was originally discovered in a Si MOSFET (this stands for “metal-oxide-semiconductor field-effect transistor”). This is a metal-insulatorsemiconductor sandwich, with electrons trapped in the “inversion band” of width ∼ 30 Å between the insulator and semi-conductor. Meanwhile the fractional quantum Hall effect was discovered in a GaAs-GaAlAs heterostructure. A lot of the subsequent work was done on this system, and it usually goes by the name GaAs (Gallium Arsenide if your chemistry is rusty). In both these systems, the density of electrons is around n ∼ 10¹¹ − 10¹² cm⁻². More recently, both quantum Hall effects have been discovered in graphene, which is a two dimensional material with relativistic electrons. The physics here is similar in spirit, but differs in details.

There were several major steps in the theory of the FQHE.

• Laughlin states and fractionally-charged quasiparticles: this theory, proposed by Laughlin, is based on accurate trial wave functions for the ground state at fraction 1/q as well as its quasiparticle and quasihole excitations. The excitations have fractional charge of magnitude e* = e/q
  
• Fractional exchange statistics of quasiparticles: Bertrand Halperin conjectured, and Daniel Arovas, J. R. Schrieffer, and Frank Wilczek demonstrated, that the fractionally charged quasiparticle excitations of the Laughlin states are anyons with fractional statistical angle θ = π/q; the wave function acquires phase factor of e^iθ (together with an Aharonov-Bohm phase factor) when identical quasiparticles are exchanged in a counterclockwise sense. A recent experiment seems to give a clear demonstration of this effect.
  
• Hierarchy states: this theory was proposed by Duncan Haldane, and further clarified by Halperin, to explain the observed filling fractions not occurring at the Laughlin states' v = 1/q. Starting with the Laughlin states, new states at different fillings can be formed by condensing quasiparticles into their own Laughlin states. The new states and their fillings are constrained by the fractional statistics of the quasiparticles, producing e.g. v = 2/5 and 2/7 states from the Laughlin v = 1/3 state. Similarly constructing another set of new states by condensing quasiparticles of the first set of new states, and so on, produces a hierarchy of states covering all the odd-denominator filling fractions. This idea has been validated quantitatively, and brings out the observed fractions in a natural order. Laughlin's original plasma model was extended to the hierarchy states by MacDonald and others.
  
• Composite fermions: this theory was proposed by Jain, and further extended by Halperin, Lee and Read. The basic idea of this theory is that as a result of the repulsive interactions, two (or, in general, an even number of) vortices are captured by each electron, forming integer-charged quasiparticles called composite fermions. The fractional states of the electrons are understood as the integer QHE of composite fermions. For example, this makes electrons at filling factors 1/3, 2/5, 3/7, etc. behave in the same way as at filling factor 1, 2, 3, etc. Composite fermions have been observed, and the theory has been verified by experiment and computer calculations. Composite fermions are valid even beyond the fractional quantum Hall effect; for example, the filling factor 1/2 corresponds to zero magnetic field for composite fermions, resulting in their Fermi sea.
  

Fractionally charged quasiparticles are neither bosons nor fermions and exhibit anyonic statistics. The fractional quantum Hall effect continues to be influential in theories about topological order. Certain fractional quantum Hall phases appear to have the right properties for building a topological quantum computer.

Impact of fractional quantum Hall effect

The FQH effect shows the limits of Landau's symmetry breaking theory. Previously it was long believed that the symmetry breaking theory could explain all the important concepts and essential properties of all forms of matter. According to this view the only thing to be done is to apply the symmetry breaking theory to all different kinds of phases and phase transitions. From this perspective, we can understand the importance of the FQHE discovered by Tsui, Stormer, and Gossard.

Different FQH states all have the same symmetry and cannot be described by symmetry breaking theory. Thus FQH states represent new states of matter that contain a completely new kind of order—topological order. For example, properties once deemed isotropic for all materials may be anisotropic in 2D planes. The existence of FQH liquids indicates that there is a whole new world beyond the paradigm of symmetry breaking, waiting to be explored. The FQH effect opened up a new chapter in condensed matter physics. The new type of orders represented by FQH states greatly enrich our understanding of quantum phases and quantum phase transitions. The associated fractional charge, fractional statistics, non-Abelian statistics, chiral edge states, etc. demonstrate the power and the fascination of emergence in many-body systems.

Honorable mention: Landau Levels

In two dimensions, when classical electrons are subjected to a magnetic field they follow circular cyclotron orbits. When the system is treated quantum mechanically, these orbits are quantized. The energy levels of these quantized orbitals take on discrete values:

E_n = ħω_c( n + ½)

where ω_c = eB/m is the cyclotron frequency. These orbitals are known as Landau levels, and at weak magnetic fields, their existence gives rise to many "quantum oscillations" such as the Shubnikov–de Haas oscillations and the de Haas–van Alphen effect (which is often used to map the Fermi surface of metals). For strong magnetic fields, each Landau level is highly degenerate (i.e. there are many single particle states which have the same energy E_n). Specifically, for a sample of area A, in magnetic field B, the degeneracy of each Landau level is

N = g_sBA/ ϕ0

where g_s represents a factor of 2 for spin degeneracy, and ϕ₀ ≈ 2×10⁻¹⁵ Wb is the magnetic flux quantum. For sufficiently strong magnetic fields, each Landau level may have so many states that all of the free electrons in the system sit in only a few Landau levels; it is in this regime where one observes the quantum Hall effect.

RESUME

The quantum Hall effect (or integer quantum Hall effect) is a quantum-mechanical version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductance σ undergoes quantum Hall transitions to take on the quantized values

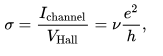
where I_channel is the channel current, V_Hall is the Hall voltage, e is the elementary charge and h is Planck's constant. The prefactor ν is known as the filling factor, and can take on either integer (ν = 1, 2, 3,…) or fractional (ν = 1/3, 2/5, 3/7, 2/3, 3/5, 1/5, 2/9, 3/13, 5/2, 12/5,…) values. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether ν is an integer or fraction, respectively.

The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level is in a clean spectral gap, this situation corresponds to one where the Fermi level is an energy with a finite density of states, though these states are localized.

The fractional quantum Hall effect is more complicated, as its existence relies fundamentally on electron–electron interactions. The fractional quantum Hall effect is also understood as an integer quantum Hall effect, although not of electrons but of charge-flux composites known as composite fermions. In 1988, it was proposed that there was quantum Hall effect without Landau levels. This quantum Hall effect is referred to as the quantum anomalous Hall (QAH) effect. There is also a new concept of the quantum spin Hall effect which is an analogue of the quantum Hall effect, where spin currents flow instead of charge currents.

REFERENCES

University of Cambridge. Available in: http://www.damtp.cam.ac.uk/user/tong/qhe/qhe.pdf. Access in: 27/10/2018.

American Physical Society. Available in: https://physics.aps.org/articles/v8/41. Access in: 27/10/2018.

Wikipedia. Available in: https://en.wikipedia.org/wiki/Quantum_Hall_effect. Access in: 27/10/2018.

Wikipedia. Available in: https://en.wikipedia.org/wiki/Fractional_quantum_Hall_effect. Access in: 27/10/2018.