



P.A.M. Dirac.
P.A.M. Dirac, in full Paul Adrien Maurice Dirac, English theoretical physicist who was one of the founders of quantum mechanics and quantum electrodynamics. Dirac is most famous for his 1928 relativistic quantum theory of the electron and his prediction of the existence of antiparticles. In 1928 Dirac published what may be his greatest single accomplishment — the relativistic wave equation for the electron. In order to satisfy the condition of relativistic invariance (i.e., treating space and time coordinates on the same footing), the Dirac equation required a combination of four wave functions and relatively new mathematical quantities known as spinors. As an added bonus, the equation described electron spin (magnetic moment)—a fundamental but theretofore not properly explained feature of quantum particles.
This theory is applicable to massive particles propagating at all velocities up to those comparable to the speed of lightc, and can accommodate massless particles. The theory has application in high energy physics, particle physics and accelerator physics, as well as atomic physics, chemistry and condensed matter physics.
In physics, relativistic quantum mechanics (RQM) is the quantum mechanics applied with special relativity, but not general relativity. Although the earlier formulations, like the Schrödinger picture and Heisenberg picture were originally formulated in a non-relativistic background, these pictures of quantum mechanics also apply with special relativity.
The relativistic formulation is more successful than the original quantum mechanics in some contexts, in particular: the prediction of antimatter, electron spin, spin magnetic moments of elementary spin 1/2 fermions, fine structure, and quantum dynamics of charged particles in electromagnetic fields. The key result is the Dirac equation, from which these predictions emerge automatically. By contrast, in quantum mechanics, terms have to be introduced artificially into the Hamiltonian operator to achieve agreement with experimental observations. It was validated by accounting for the fine details of the hydrogen spectrum in a completely rigorous way.
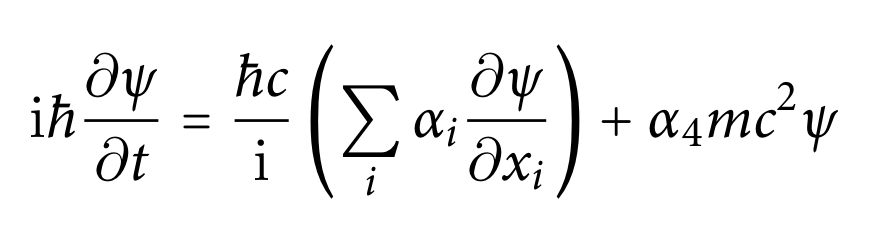
Dirac equation (original).
The equation also implied the existence of a new form of matter, antimatter, previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a theoretical justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin; the wave functions in the Dirac theory are vectors of four complex numbers (known as bispinors), two of which resemble the Pauli wavefunction in the non-relativistic limit, in contrast to the Schrödinger equation which described wave functions of only one complex value.
Nevertheless, RQM is only an approximation to a fully self-consistent relativistic theory of known particle interactions because it does not describe cases where the number of (elementary) particles changes; for example in matter creation and annihilation. By yet another theoretical advance, a more accurate theory that allows for these occurrences and other predictions is relativistic quantum field theory in which particles are interpreted as field quanta.
His contribution to quantum mechanics, through his formulation, implied a change to what would be the electronic levels and the atomic model (electronic cloud).

Hydrogen atom for Bohr, Schrödinger and Dirac, respectively.
REFERENCES
Encyclopædia Britannica. Available in: https://www.britannica.com/biography/Paul-Dirac. Access in: 17/09/2018.
Encyclopædia Britannica. Available in: https://www.britannica.com/science/Dirac-equation. Access in: 17/09/2018.
Wikipedia. Available in: https://en.wikipedia.org/wiki/Dirac_equation. Access in: 17/09/2018.
Wikipedia. Available in: https://en.wikipedia.org/wiki/Relativistic_quantum_mechanics. Access in: 17/09/2018.

Default timespace