



Collective model, also called unified model, description of atomic nuclei that incorporates aspects of both the shell nuclear model and the liquid-drop model to explain certain magnetic and electric properties that neither of the two separately can explain.
Aage Bohr, the son of Niels Bohr, worked with Ben R. Mottelson, a Danish-American physicist, to relate collective properties of nuclei to the motion of their constituent nucleons. James Rainwater also worked on this topic and the three; Bohr, Mottelson and Rainwater; received the Nobel Prize in Physics in 1975.

.
At the time the three started working there was a fixation with deriving everything from the Schrödinger Equation. Instead Bohr and Mottelson wanted their analysis tied to empirical fact. They asserted
Progress in this direction has been achieved by a combination of approaches based partly on clues provided by experimental data, partly on the theoretical study of model systems, and partly on the exploration of general relations following from considerations of symmetry.
They planned for a three volume presentation but that devolved to two volumes; Volume I covering single-particle motion and and Volume II nuclear deformations.
The authors state in Volume I that the nuclei are relatively weakly bound systems.
The energy required to remove a nucleon from a nucleus is about 5-10 MeV, and the average kinetic energy of the nucleons in a nucleus is of the order of 25 MeV. These energies are small compared with the rest energies of the nucleons themselves (Mc² ≅ 1000 MeV), but also of the lightest of the hadrons, the π mesons (mπc² ≅ 137 MeV). In the analysis of nuclear bound states and reactions at not too high energies, it therefore a good approximation to regard the nucleus as composed of a definite number of nucleons with properties similar to those of free nucleons, and moving with nonrelativistic velocities (v²/c² ≤ 0.1).
Aage Bohr, in a lecture given at the Danish Society for the Dissemination of Natural Science, gave the following sketch of the Collective Model of Nuclear Structure:
Though the investigation of different properties of nuclei, one thus is led to two widely different pictures of nuclear structure corresponding to the liquid-drop model and to the shell model. It is, nevertheless, not difficult to combine the most essential features of both models. […]
In the shell model one regards the orbital motion of the individual nucleons in the average nuclear field as the primary form of motion; in the liquid-drop model one looks at the simple collective motions of the nucleons. Both of these forms of motion are observed experimentally in nuclei, so one is led to seek a more general description of nuclear structure by considering the total state of motion as a superposition of the two previously mentioned basic components.
Such a description may be regarded as a generalization of the shell model in which the nuclear field, previously considered constant, is now to be considered to be a dynamic variable; the variation of the collective nuclear field is linked with the vibrating shape of the nucleus.
In the shell model, nuclear energy levels are calculated on the basis of a single nucleon (proton or neutron) moving in a potential field produced by all the other nucleons. Nuclear structure and behaviour are then explained by considering single nucleons beyond a passive nuclear core composed of paired protons and paired neutrons that fill groups of energy levels, or shells. In the liquid-drop model, nuclear structure and behaviour are explained on the basis of statistical contributions of all the nucleons (much as the molecules of a spherical drop of water contribute to the overall energy and surface tension).
In the collective model, high-energy states of the nucleus and certain magnetic and electric properties are explained by the motion of the nucleons outside the closed shells (full energy levels) combined with the motion of the paired nucleons in the core. Roughly speaking, the nuclear core may be thought of as a liquid drop on whose surface circulates a stable tidal bulge directed toward the rotating unpaired nucleons outside the bulge. The tide of positively charged protons constitutes a current that in turn contributes to the magnetic properties of the nucleus. The increase in nuclear deformation that occurs with the increase in the number of unpaired nucleons accounts for the measured electric quadrupole moment, which may be considered a measure of how much the distribution of electric charge in the nucleus departs from spherical symmetry.
In addition to individual nucleons changing orbits to create excited states of the nucleus as described by the Shell Model, there are nuclear transitions that involve many (if not all) of the nucleons. Since these nucleons are acting together, their properties are called collective, and their transitions are described by a Collective Model of nuclear structure. High-mass nuclei have low-lying excited states that are described as vibrations or rotations of nonspherical nuclei. Many of these collective properties are similar to those of a rotating or vibrating drop of liquid, and in its early development the Collective Model. The first important application of the Liquid-Drop model was in the analysis of nuclear fission, in which a massive nucleus splits into two lower-mass fragments. The model calculates an energy barrier to fission as a sum of the repulsive Coulomb forces between the protons of the nucleus and the attractive surface tension of the skin of the "liquid drop" nucleus. If the barrier is low enough the nucleus might fission spontaneously. For higher barriers, it takes a nuclear reaction to induce fission.
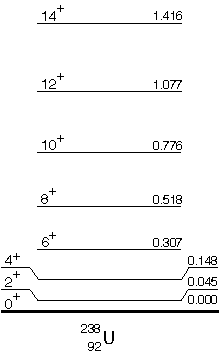
The energy level of uranium-238.
The figure above shows the energy levels of 238U. The quantum numbers, level spacings, and gamma ray transition probabilities identify these levels as rotational states of a nonspherical nucleus. Nuclei showing collective properties are usually those with many valence nucleons, that is, those with proton or neutron numbers that are far from filled shells. As with the Shell Model, the Collective Model permits the calculation of spin-parity assignments and transition probabilities that are in good agreement with the measured properties of collective nuclei.
REFERENCES
Berkeley Lab. Available in: http://www2.lbl.gov/abc/wallchart/chapters/06/2.html. Access in: 04/10/2018.
Encyclopaedia Britannica. Available in: https://www.britannica.com/science/collective-model. Access in: 04/10/2018.
San José State University. Available in: http://www.sjsu.edu/faculty/watkins/bohraage.htm. Access in: 04/10/2018.

Default timespace